逻辑回归的定义
简单来说,逻辑回归是一种用于解决二分类问题的机器学习算法。
逻辑回归与线性回归的关系:
- 两者都是广义的线性模型
- 逻辑回归因变量y服从伯努利分布,线性回归因变量y服从高斯分布
- 逻辑回归中通过sigmod函数引入非线性因素,从而轻松解决0/1分类问题
假设函数(Hypothesis function)
逻辑回归的假设函数形式:
其中x是我们的输入,${\theta}$是要求取的参数。
sigmod函数,也称为逻辑函数,曲线如下: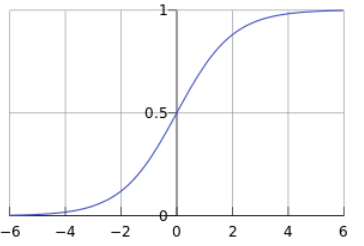
一个机器学习模型,实际上是把决策函数限定在某一组条件下,这组限定条件(简单合理)就决定了模型的假设空间。逻辑回归模型的假设:
决策边界(decision boundary)
决策边界,也称决策面,是用于在N维空间,将不同样本分开的平面或者曲面。
Note:决策边界是假设函数的属性,由参数决定,而不是由数据集决定。
- 线性决策边界:
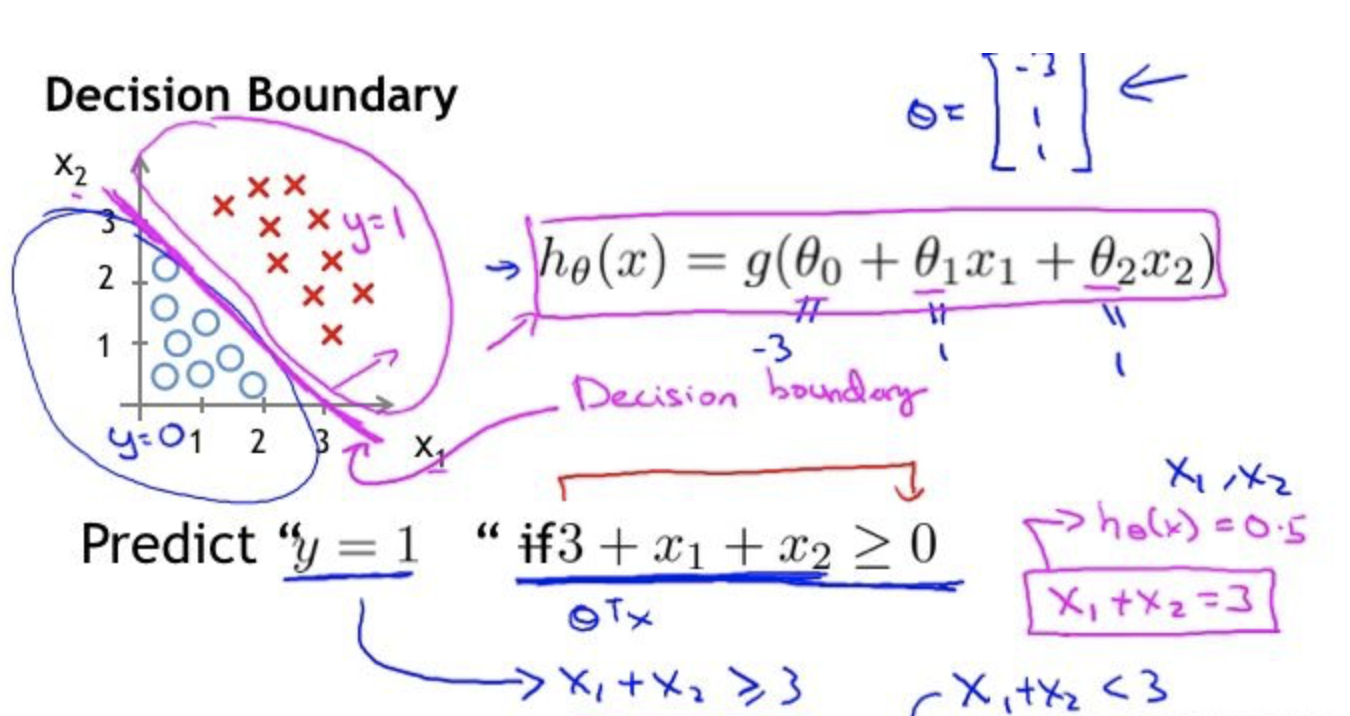
- 非线性边界:

代价函数(cost function)
什么是代价函数
假设有训练样本(x,y),模型为h,参数为θ。概况来讲,任何衡量预测值h(θ)和真实值y之间差异的函数都可以称为代价函数C(θ)。
如果由多个样本,则可以将所有代价函数的值求均值,记为J(θ)。因此,可以得出代价函数具有以下性质:
- 择代价参数时,最好选择对参数θ可微的函数
- 代价函数是θ的函数,对于每一个算法代价函数不是唯一的
- 总的代价函数J(θ)评价模型的好坏,代价函数越小说明模型和参数越符合训练样本
训练参数的过程就是不断改变θ,从而得到更小的J(θ)的过程。理性情况下,当取到代价函数J的最小值时,就得到了最优参数θ,记为:$\min _{\theta} J(\theta)$.
c参数优化:最常用的方法时梯度下降,这里的梯度就是代价函数J(θ)对θ1,……,θn的偏导数。
代价函数的常见形式
在线性回归中,最常用的是
均方误差(Mean squared error),即:m:训练样本的个数
$h_{\theta}(x)$:用参数${\theta}$和x预测出来的y值
y:原训练样本中的y值在逻辑回归中,最常用的代价函数是交叉熵。
逻辑回归的代价函数:对于单个样本,J(θ)对应的C(θ):
上面的方程等价于:
代价函数与梯度
梯度下降中的梯度指的是代价函数对各个参数的偏导数,偏导数的方向决定了在学习过程中参数下降的方向,学习率(通常用α表示)决定了每步变化的步长,有了导数和学习率就可以使用梯度下降算法(Gradient Descent Algorithm)更新参数, 即求解使J(θ)值最小的θ:

