c++排序总结

2020-09-08

最近在leetcode上做题的时候遇到一些排序变形的题，这篇文章把基础的排序做一个总结。

排序算法简述

1.分类

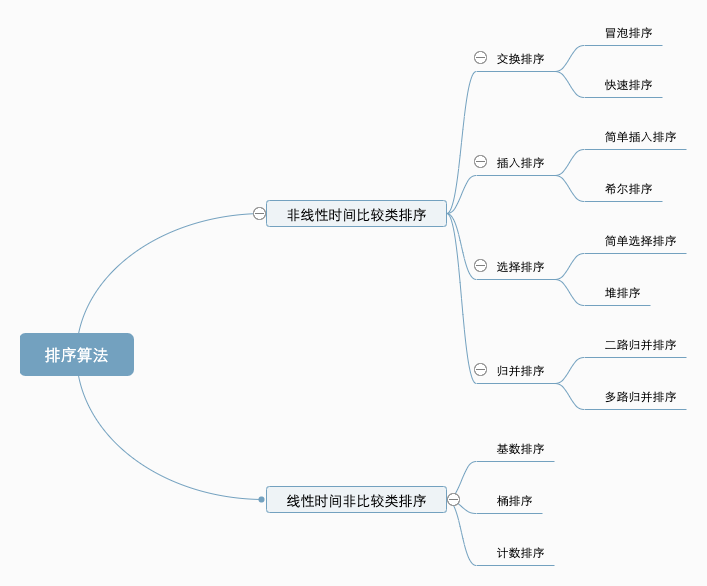
10种常见的排序算法可以分为两类：

非线性时间排序算法：通过比较决定元素的相对次序，时间复杂度下界为O(nlogn),非线性时间运行。
线性时间排序算法：不通过比较来决定元素的相对次序，可以突破非线性时间排序的时间下界，以线性时间运行。

2.算法复杂度

排序算法	时间复杂度(平均)	时间复杂度(最坏)	时间复杂度(最好)	空间复杂度	稳定性
插入排序	$O\left(n^{2}\right)$	$O\left(n^{2}\right)$	$O\left(n\right)$	$O(1)$	稳定
希尔排序	$O\left(n^{1.3}\right)$	$O\left(n^{2}\right)$	$O\left(n\right)$	$O(1)$	不稳定
选择排序	$O\left(n^{2}\right)$	$O\left(n^{2}\right)$	$O\left(n\right)$	$O(1)$	不稳定
堆排序	$O\left(n \log _{2} n\right)$	$O\left(n \log _{2} n\right)$	$O\left(n \log _{2} n\right)$	$O(1)$	不稳定
冒泡排序	$O\left(n^{2}\right)$	$O\left(n^{2}\right)$	$O\left(n\right)$	$O(1)$	稳定
快速排序	$O\left(n \log _{2} n\right)$	$O\left(n^{2}\right)$	$O\left(n \log _{2} n\right)$	$O\left(n \log _{2} n\right)$	不稳定
归并排序	$O\left(n \log _{2} n\right)$	$O\left(n \log _{2} n\right)$	$O\left(n \log _{2} n\right)$	$O(n)$	稳定

基数排序	$O\left(n^{*} k\right)$	$O\left(n^{*} k\right)$	$O\left(n^{*} k\right)$	$O\left(n{+} k\right)$	稳定
桶排序	$O\left(n{+} k\right)$	$O\left(n{+} k\right)$	$O\left(n{+} k\right)$	$O\left(n{+} k\right)$	稳定
计数排序	$O\left(n{+} k\right)$	$O\left(n{+} k\right)$	$O\left(n{+} k\right)$	$O\left(n{+} k\right)$	稳定

排序算法实现

1.冒泡排序

冒泡排序是比较相邻数据，如果反序则交换。第一遍扫描最大的数在数组最后，第二遍第2大的数放在倒数第二的位置……，直至n-1遍，排序完成。

void BubbleSort(int* a,int len){
    if(a==NULL||len<=1) return;
    for(int i=0;i<len-1;i++){
        for(int j=0;j<len-i-1;j++){
            if(a[j]>a[j+1]){
                a[j]=a[j]^a[j+1];
                a[j+1]=a[j]^a[j+1];
                a[j]=a[j]^a[j+1];
                //swap(a[j],a[j+1])
            } 
        }
    }
    return;
}

2.快速排序

快速排序设置left和right指针，和基准值base(一般取数组left位置的数，随机选取可以与left数据交换后进行快排)。left向后找比base大的数，right向前找比base小的数，然后进行交换，重复上述步骤直至left，right重合。此时数组分为两个部分：比base大的部分和小的部分，再对这两个部分进行快排……，最终快排完成。

void QuickSort(int* a,int left,int right){
    if(left>=right) return;
    int i=left,j=right,base=a[left];
    while(i<j){
        while(a[j]>=base&&i<j) j--;
        if(i<j) a[i++]=a[j];
        while(a[i]<=base&&i<j) i++;
        if(i<j) a[j]=a[i];
    }
    a[i]=base;
    QuickSort(a,left,i-1);
    QucickSort(a,i+1,right);
}

3.直接插入排序

直接插入排序的思想：对于一个数组A[0,n]的排序问题，假设A[0,n-1]排序问题已经解决，考虑A[n]的值，从右向左扫描数组，直到第一个小于等于A[n]的元素，将A[n]插入这个元素后面。

void InsertSort(int* a,int len){
    if(len<=1) return;
    for(int i=1;i<len;i++){
        for(int j=i;j>0;--j){
            if(a[j]<=a[j-1]){//升序 a[j]>=a[j-1]:降序
                swap(a[j],a[j+1]);
            }else{
                break;
            }
        }
    }
    return;
}

4.希尔排序

希尔排序也是一种插入排序，也称缩小增量排序。希尔排序是把元素按照下标的一定增量分组，对每一组使用直接插入排序；随着增量逐渐减小，每组的元素越来越多，当增量为1时，整个数组被分为一组，算法结束。

void ShellSort(int* a,int len){
    if(len<=1) return;
    for(int gap=len/2;gap>=1;gap=/2){//增量
        for(int k=0;k<gap;k++){//分组
            for(int i=k+gap;i<len;i+=gap){//简单插入排序
                for(int j=i;j>k;j-=gap){
                    if(a[j]<a[j-gap]){
                        swap(a[j],a[j-gap]);
                    }else{
                        break;
                    }
                }
            }
        }
    }
    return;

}

5.选择排序

选择排序是一种简单直观的排序方法。初始时在序列中找到最小(大)元素，放到序列最前面作为已排序序列；然后，从剩余未排序元素中继续寻找最小(大)的元素，放在已经排序序列的末尾，直至排序结束。

void SelectSort(int* a,int len){
    if(len<=1) return;
    int index;//记录最值的位置
    for(int i=0;i<len-1;i++){
        index=i;
        for(int j=i+1;j<len;j++){
            if(a[j]<a[index]) index=i;
        }
        swap(a[i],a[index]);
    }
    return;
}

6.堆排序

堆实际上是一棵完全二叉树。堆的每一个父节点大于或者小于其子节点，堆的每一个左子树和右子树也是一个堆。堆分为大顶堆和小顶堆。堆的一般用数组存储，i节点的父节点的下标是(i-1)/2,左右子节点的下标分别是2i+1,2i+2.
堆排序分为3个步骤：

建堆(升序：大堆；降序：小堆)
交换数据

向下调整

//调整
void AdjustHeap(int* a,int node,int len){
    //node是需要调整的节点下标
    int index=node;
    int child=2*child+1;//左孩子
    while(child<len){
        if(child+1<len&&a[child]<a[child+1]) child++;//判断左右节点的较大值
        if(a[index]>=a[child]) break;
        swap(a[index],a[child]);
        index=child;
        child=2*index+1;
    }
}
//建堆
void MakeHeap(int* a,int len){
    for(int i=0;i<len/2;i--){
        AdjustHeap(a,i,len);
    }
}
//排序
void HeapSort(int* a,int len){
    MakeHeap(a,len);
    for(int i=len-1;i>=0;i--){
        swap(a[i],a[0]);
        AdjustHeap(a,0,i);
    }
}

7.归并排序

归并排序采用经典的分治思想(divide-and-conquer),divide是问题分解成小的问题递归求解,conquer再把子问题的答案合并起来。

void Merge(int* a,int begin,int mid,int end){
    int i=begin,j=mid+1,k=0;
    int len=end-begin+1;
    int* tmp=new int[len];
    while(i<=mid&&j<=end) tmp[k++]=a[i]<=a[j]?a[i++]:a[j++];
    while(i<=mid) tmp[k++]=a[i++];
    while(j<=end) tmp[k++]=a[j++];
    for(int k=0;k<len;k++) a[begin+k]=tmp[k];
    delete[] tmp;
}

void MergeSort(int* a,int begin,int end){
    if(begin==end) return;
    int mid=(begin+end)>>1;
    MergeSort(a,begin,mid);
    MergerSort(a,mid+1,end);
    Merge(a,begin,mid,end);
}

george.zhang